Rumus Luas Dan Keliling Bangun Datar lengkap dan gambarnya

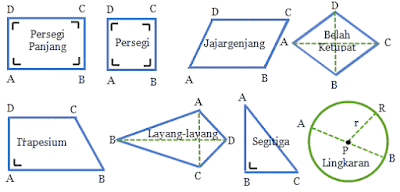
Setelah kemarin kita membahas mengenai sifat-sifat bangun datar kali ini tema pembahasan kita adalah tentang rumus bangun datar lengkap. Menurut situs enslikopedia bebas wikipedia bangun datar adalah sebutan bagi bangun-bangun dua dimensi, seperti lingkaran, belah ketupat, layang-layang, trapesium, jajar genjang, segitiga, persegi panjang dan persegi. Masing-masing dari bangun tersebut mempunyai rumus untuk menghitung luas dan keliling yang berbeda satu dengan yang lain. Berikut ini rumus-rumusnya :

Rumus Bangun Datar

1. Persegi 

Rumus luas persegi adalah

L = s²

Dimana :
L = luas
s = sisi persegi

Rumus keliling persegi yaitu

K = 4.s

Dimana
K = keliling
s = ukuran sisi

2. Persegi Panjang

Rumus luas persegi panjang adalah

L =  p x l 

Dimana
L = luas
p = panjang
l = lebar

Rumus keliling persegi panjang adalah

K = (2 x p) + (2 x l)

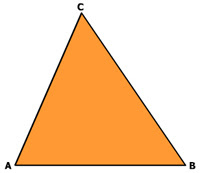
3. Segitiga

Rumus luas segitiga adalah

L = 1/2 x a x t

dimana :
a = panjang alas
t = tinggi

Rumus keliling sebuah segitiga yaitu


K = panjang sisi1 + panjang sisi2 + panjang sisi3 ( atau jumlah semua sisinya )

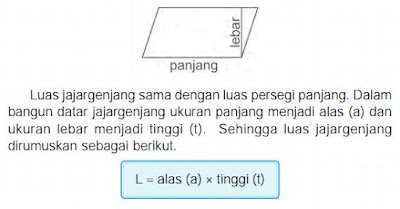
4. Jajar Genjang

Rumus luas jajar genjang adalah

L = alas x tinggi

Keterangan :
L = luas jajar genjang
alas = panjang alas
tinggi = panjang tinggi

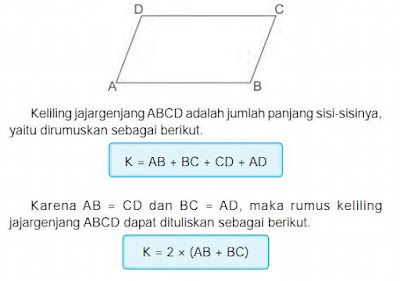
Rumus keliling jajar genjang adalah


K = 2 x alas + 2 x sisi miring ( atau jumlah semua sisinya )

5. Trapesium

Rumus luas trapesium adalah

Luas Trapesium =    1/2 x jumlah sisi sejajar x tinggi

Keterangan :
Jumlah sisi sejajar = A + B ( lihat gambar di atas  )
Tinggi =  t ( lihat gambar  di atas )

Rumus keliling trapesium adalah

Keliling Trapesium = jumlah seluruh sisi-sisinya

Keterangan :
Keliling trapesium merupakan jumlah seluruh sisi-sisinya

6. Layang-layang

Rumus luas layang-layang adalah

Luas = ½ . d1 x d2

Dimana
d1 =diagonal vertikal
d2 = diagonal horizontal

Rumus keliling layang-layang adalah

Keliling = 2.s1 + 2.s2

atau

Keliling = 2 ( s1 + s2 )

Keliling bangun layang-layang diperoleh dengan menjumlahkan panjang semua sisi-sisinya.

7. Belah Ketupat

Rumus luas belah ketupat adalah

Luas = ½ x diagonal 1 x diagonal 2 

Rumus keliling belah ketupat adalah

Keliling = s + s + s +s  atau Keliling = 4 x sisi

8. Lingkaran

Rumus luas lingkaran adalah

Luas Lingkaran  = π x r2

Dimana
π ( phi ) = 3,14 atau 22/7
r  = jari-jari dari lingkaran atau setengah diameter lingkaran, jika jari-jari satuannya centimeter (cm)
maka satuan luasnya cm2.

Rumus keliling lingkaran adalah

Keliling = π x d 
Atau karena d = 2 x r , maka di dapat K = π x 2 x jari-jari
Dimana
d = diameter
r = jari-jari
π = 22/7 atau 3.14

Demikian pembahasan mengenai rumus menghitung luas dan keliling bangun datar lengkap semoga bermanfaat bagi semua.[]

Related Posts:

Tweet

Sifat-sifat Bangun Datar Lengkap

Pada pertemuan kali ini blog rumus matematika akan membahas mengenai sifat-sifat bangun datar. Apa itu sih bangun datar ? Bangun datar merupakan penamaan bagi kelompok bangun-bangun dua dimensi seperti persegi, persegi panjang, segitiga, jajar genjang, trapesium, layang-layang, belah ketupat dan lingkaran. Tiap-tiap bangun datar tersebut mempunyai ciri-ciri dan sifat yang berbeda satu dengan yang lain. Berikut ini pembahasan lengkap mengenai sifat-sifat bangun datar.

Sifat-sifat Bangun Datar Persegi

1. Semua sisi-sisinya panjangnya sama dan semua sisinya berhadapan sejajar.
2. Setiap sudut yang dimilikinya siku-siku.
3. Mempunyai dua diagonal yang panjangnya sama dan berpotongan di tengah-tengah serta membentuk sudut siku-siku.
4. Setiap sudutnya di bagi dua sama besarnya oleh diagonalnya.
5. Mempunyai empat buah sumbu simetri. ( Baca juga rumus persegi )

Sifat-sifat Bangun Datar Persegi Panjang

1. Setiap sisi-sisi yang berhadapan mempunyai ukuran sama panjang dan sejajar.
2. Semua sudutnya adalah sudut siku-siku.
3. Memiliki dua buah diagonal yang sama panjang dan saling berpotongan di titik pusat bangun persegi panjang, Titik tersebut membagi dua bagian diagonal dengan sama panjang.
4. Memiliki dua buah sumbu simetri yaitu sumbu vertikal dan sumbu horizontal. ( Baca juga rumus persegi panjang )

Sifat-sifat Bangun Datar Segitiga

1. Memiliki tiga buah titik sudut dan tiga buah sisi.
2. Jumlah besar semua sudutnya adalah 180 derajat. ( Baca juga sifat segitiga sama kaki, segitiga sama sisi, segitiga sembarang dan segitiga siku-siku )

Sifat-sifat Bangun Datar Jajar genjang

1. Sisi-sisi yang berhadapan ukurannya sama panjang dan sejajar.
2. Sudut-sudut yang berhadapan besarnya sama.
3. Memiliki dua buah diagonal yang berpotongan di satu titik dan saling membagi dua sama panjang.
4. Mempunyai simetri putar tingkat dua.
5. Tidak memiliki simetri lipat. ( Baca juga rumus jajar genjang )

Sifat-sifat Bangun Datar Trapesium

1. Mempunyai 4 buah sisi dan 4 buah titik sudut.
2. Mempunyai satu pasang sisi yang sejajar tetapi panjangnya tidak sama.
3. Mempunyai sudut di antara sisi sejajarnya besarnya 180°. ( Baca juga rumus trapesium dan jenis-jenis trapesium )

Sifat-sifat Bangun Datar Layang-layang

1. Memiliki 2 pasang sisi yang panjang sama.
2. Memiliki satu pasang sudut yang berhadapan yang besarnya sama.
3. Memiliki 4 titik sudut.
4. Diagonal-diagonalnya saling berpotongan tegak lurus.
5. Salah satu diagonal bangun ini membagi dua sama panjang diagonal yang lain.
6. Hanya memiliki satu buah simetri lipat. ( Baca juga rumus layang-layang )

Sifat-sifat Bangun Datar Belah Ketupat

1. Ukuran sisi-sisinya panjangnya sama.
2. Sudut-sudut yang berhadapan sama besar serta dibagi dua oleh diagonalnya dengan sama besar.
3. Diagonalnya saling iberpotongan sama panjang dan saling tegak lurus.
4. Terdapat 2 buah sumbu simetri.
5. Diagonal-diagonalnya adalah sumbu simetrinya.
6. Terdapat 2 simetri lipat.
7. Terdapat 2 simetri putar. 
   ( Baca juga rumus belah ketupat )

Sifat-sifat Bangun Datar Lingkaran

1. Memiliki simetri putar tak terhingga.
2. Memiliki simetri lipat serta sumbunya yang tak terhingga.
3. tidak mempunyai titik sudut.
4. Mempunyai satu buah sisi. 

Demikian pembahasan mengenai Sifat-sifat Bangun Datar Lengkap semoga dapat menambah wawasan pengetahuan kita semua.[]

Related Posts:

Tweet

Sifat-sifat Bangun Belah Ketupat

Sifat-sifat Belah Ketupat - Belah ketupat merupakan salah satu jenis bangun datar dua dimensi. Dinamakan belah ketupat mungkin karena bangun datar ini mirip dengan ketupat yang sering kita jumpai saat lebaran, iya ngak ?

Setelah pada artikel sebelumnya sudah membahas mengenai rumus luas dan keliling belah ketupat pada kesempatan kali ini kami akan mencoba berbagi tentang ciri-ciri belah ketupat.

gambar bangun belah ketupat

Berikut ini merupakan sifat-sifat belah ketupat :

1. Semua ukuran sisi-sisinya sama panjang.
2. Sudut-sudut yang berhadapan besarnya sama dan di bagi dua sama besar oleh diagonal-diagonalnya,
3. Kedua diagonalnya saling membagi dua sama panjang dan saling tegak lurus satu sama lainnya.
4. Mempunyai dua buah sumbu simetri.
5. Kedua diagonalnya merupakan sumbu simetri dari bangun belah ketupat.
6. Memiliki dua simetri lipat.
7. Memiliki dua buah simetri putar.
8. Jumlah semua sudutnya besarnya adalah 360 derajat.


Demikian beberapa ciri-ciri belah ketupat lengkap semoga bermanfaat bagi pembaca semua.[]

Related Posts:

Tweet

Rumus Luas Dan Keliling Belah Ketupat

Rumus Luas Dan Keliling Bangun Belah Ketupat - Belah ketupat adalah sebuah bangun datar dua dimensi yang terbentuk oleh 4 buah rusuk yang panjang sama dan mempunyai 2 pasang sudut bukan siku-siku yang masing-masing besarnya sama dengan sudut  yang ada di hadapannya.

Belah ketupat juga bisa terbentuk dari dua buah segitiga sama kaki dan bayangannya, dengan alas sebagai sumbu cermin.

Bila kita perhatikan gambar bangun belah ketupat ABCD di atas kita akan melihat jika bangun belah ketupat mirip dengan bangun layang layang( Baca rumus layang-layang ). Perbedaannya terdapat pada ukuran panjang sisi-sisinya, pada belah ketupat ukuran panjang sisi-sisinya sama panjang semuanya dan pada layang-layang terdapat dua sisi yang panjangnya sama.

Setelah melihat gambar di atas kita memperoleh informasi yaitu kode s merupakan sisi dari belah ketupat, d1 merupakan diagonal horizontalnya dan d2 merupakan diagonal vertikalnya, kedua diagonal tersbut saling berpotongan secara tegak lurus. Selain itu juga pada bangun belah ketupat terdapat dua buah pasang sudut yang sama besarnya yaitu sudut A = sudut C dan sudut B = sudut D.

Rumus Luas Dan Keliling Belah Ketupat dan Contoh Soalnya

Untuk menghitung ukuran luas dari sebuah bangun datar belah ketupat, dapat menggunakan rumus:

Luas = ½ x diagonal 1 x diagonal 2 

Sedangkan untuk menghitung ukuran keliling dari bangun datar belah ketupat, kita dapat memakai persamaan rumus:

Keliling = s + s + s +s 

Keliling = 4 x sisi


Berikut ini ada beberapa contoh penggunaan rumus dalam beberapa contoh soal di bawah ini silahkan kamu simak selengkapnya.

1. Hitunglah ukuran keliling sebuah belah ketupat jika diketahui panjang sisinya adalah 10 cm.

jawab :

Keliling Belah Ketupat  = 4 x sisi
Keliling = 4 x 10 cm
Keliling = 40 cm

Jadi keliling dari bangun belah ketupat tersebut adalah 40 cm


2. Jika sebuah bangun datar belah ketupat mempunyai diagonal 12 cm dan 7 cm, Hitunglah berapa ukuran luas bangun tersebut.

Jawab :

Luas = ½ x d1 x d2
Luas = ½ x 12 x 7
Luas = ½ x 84
Luas = 42 cm²

Jadi ukuran luas bangun belah ketupat tersebut adalah 42 cm²


3. Jika sebuah belah ketupat memiliki panjang sisi 4a cm. Bila keliling dari bangun tersebut adalah 48 cm, Hitunglah berapa nilai dari a.

Jawab :

keliling = 4 x sisi
48 cm = 4 x 4a cm
48 cm = 16a cm
a = 48/16 cm
a = 3 cm

Jadi nilai a adalah 3 cm

Demikian pembahasan mengenai belah ketupat yaitu tentang Rumus Luas Dan Keliling Belah Ketupat Lengkap yang bisa kami uraikan untuk anda semoga bermanfaat bagi pembaca semua. []

Related Posts:

Tweet

Sifat sifat Bangun Layang-layang

Sifat-sifat layang-layang - Layang-layang kamu tentu sudah sangat akrab dengan bentuk bangun datar yang satu ini. Bentuk layang-layang memang serupa dan sama dengan permainan anak-anak yaitu layang-layang. Berikut ini adalah gambar layang-layang yang sering di mainkan aleh anak-anak di tanah lapang.

Menurut ensiklopedi bebas wikipedia layang-layang merupakan bangun datar dua dimensi yang terbentuk oleh dua pasang rusuk yang masing-masing pasangannya sama panjang dan saling membentuk sudut. Bagi kamu yang ingin tahu mengenai rumus luas dan keliling layang-layang kamu bisa membacanya di artikel rumus layang-layang.

Ciri-ciri Atau Sifat-sifat Layang-layang

1. Terdapatnya dua pasang sisi yang sama panjang.
2. Terdapatnya sepasang sudut berhadapan yang sama besar.
3. Terdapatnya satu sumbu simetri yang merupakan diagonal terpanjang.
4. Salah satu dari diagonalnya membagi dua sama panjang diagonal lainnya secara tegak lurus.
5. Diagonal-diagonal yang dimiliki oleh bangun layang-layang saling tegak lurus.
6. Diagonal yang menghubungkan sudut puncak membagi dua bagian sudut-sudut puncak dan layang-layang menjadi dua buah bagian yang besarnya sama.

Demikian tadi ciri-ciri bangun layang-layang semoga bermanfaat bagi pembaca semua.[]

Related Posts:

Tweet

Rumus Luas Dan Keliling Layang-Layang

Rumus layang-layang - Layang-layang adalah bangun datar dua dimensi yang dibentuk oleh dua buah segitiga sama kaki yang ukuran panjang alasnya sama panjang dan saling berhimpit. Atau menurut wikipedia layang-layang adalah sebuah bangun datar dua dimensi yang terbentuk oleh dua buah pasang rusuk yang masing-masing pasangannya sama panjang dan saling membentuk sudut.

Bangun belah ketupat merupakan bangun layang-layang yang rusuk-rusuknya sama panjang.

Bentuk bangun datar yang satu ini saya yakin sangat akrab dengan teman-teman semua karena bentuknya sama dengan layang layang yang sering kita mainkan di tanah lapang atau di sawah pada saat musim kemarau telah tiba. Oke sekarang kita kembali ke topik pembahasan, coba kamu perhatikan gambar di atas. Setelah kamu memperhatikan gambar di atas kamu akan melihat sisi layang-layang yang masing-masing di beri tanda  s1 dan s2.

Sisi s1 dan s2 masing-masing memiliki pasangan yang panjangnya sama. Sedangkan d1 dan d2 adalah diagonal dari bangun layang-layang di atas,  d1 adalah diagonal vertikal sedang d2 adalah diagonal horisontal. Untuk menghitung luas dan keliling bangun layang-layang kita memerlukan sebuah rumus, silahkan kamu simak pembahasan rumus matematika selengkapnya.

Rumus Luas Layang-layang

Luas = ½ . d1 x d2

Keterangan : d1 adalah diagonal vertikal
                      d2 adalah diagonal horizontal

Rumus Keliling Layang-layang

Keliling bangun layang-layang diperoleh dengan menjumlahkan panjang semua sisi-sisinya. Berarti rumus keliling dari layang layang adalah :

Keliling = 2.s1 + 2.s2

atau

Keliling = 2 ( s1 + s2 ).

Contoh Soal Layang-layang dan Pembahasannya

1. Jika di ketahui sebuah layang-layang memiliki panjang diagonal horizontal 10 cm dan diagonal vertikal 20 cm hitunglah berapa luas layang-layang tersebut.

Jawab :

Diagonal horizontal = d1 = 10 cm
Diagonal vertikal = d2 = 20 cm

L = 1/2 x d1 x d2
   = 1/2 x 10 cm x 20 cm
   = 1/2 x 200
   =  100 cm²

Jadi luas layang-layang tersebut adalah 100 cm².

2. Jika di ketahui sebuah layang-layang mempunyai panjang sisi yaitu s1 = 11 cm dan s2 = 13 cm. Hitunglah berapa keliling dari layang-layang tersebut.

Jawab :

K = 2(s1 + s2)
    = 2( 11 + 13 )
    = 2( 24 cm)
    = 48 cm

Jadi keliling dari layang-layang tersebut adalah 48 cm.

Demikian pembahasan singkat tentang Rumus Luas Dan Keliling Layang-Layang. Jangan lupa baca juga pembahasan sebelumnya mengenai sifat-sifat trapesium.[]

Related Posts:

Tweet

Sifat-Sifat Trapesium

Sifat-sifat trapesium atau ciri-ciri trapesium merupakan suatu bagian dari sebuah bangun trapesium yang di gunakan sebagai pembeda dengan bangun lainnya. Trapesium merupakan salah satu bangun datar dua dimensi selain persegi, persegi panjang, jajar genjang dan lainnya. Bagi teman yang ingin tahu mengenai rumus-rumus trapesium kamu bisa melihatnya disini rumus trapesium dan bagi yang inginmengetahui apa saja jenis-jenis trapesium kamu bisa membacanya disini jenis-jenis trapesium.

Berikut ini adalah beberapa ciri-ciri trapesium :

1) Jumlah sudut yang berdekatan diantara dua garis sejajar adalah 180⁰
<A + <D = 180⁰ ( Lihat gambar di atas )
<B + <C = 180⁰ ( Lihat gambar di atas )
2) Pada trapesium sama kaki, terdapat dua buah sudut yang berdekatan yang besarnya sama.
3) Pada trapesium sama kaki, terdapat diagonal yang panjangnya sama.
4) Pada trapesium sama kaki memiliki satu buah sumbu simetri.
5) Pada trapesium siku-siku memiliki dua buah sudut siku-siku.
6) Jumlah semua sudut pada trapesium adalah 360 derajat.
7) Mempunyai satu buah simetri putar.

Demikian pembahasan tentang Sifat-Sifat Trapesium semoga bermanfaat bagi teman semua salam sukses.()

Related Posts:

Tweet

Jenis-Jenis Dan Sifat-Sifat Trapesium Lengkap

Jenis-Jenis Dan Sifat-Sifat Trapesium Lengkap - Trapesium merupakan bangun segi empat yang dibentuk oleh empat buah rusuk yang dua di antaranya saling behadapan sejajar namun panjangnya tidak sama. Bangun trapesium mempunyai tiga macam jenis yaitu :

Jenis-Jenis Trapesium

1.  Trapesium Sembarang

Trapesium dapat di katakan sebagai trapesium sembarang jika trapesium tersebut tidak mempunyai kekhususan.

Sifat sifat Trapesium Sembarang

•  Mempunyai sepasang sisi sejajar yang berhadapan yang panjangnya tidak sama.
•  Mempunyai empat sudut yang besarnya tidak sama.
•  Mempunyai dua buah diagonal yang berbeda panjangnya.

2. Trapesium Siku-siku

Trapesium siku-siku merupakan sebuah bangun trapesium yang besar salah satu sudutnya adalah 90 derajat atau siku-siku.

Sifat-sifat Trapesium Siku-siku

• Mempunyai sepasang sisi sejajar yang berhadapan yang panjangnya tidak sama.
• Mempunyai dua buah sudut siku-siku yang berdekatan.
• Mempunyai dua buah diagonal yang berbeda panjangnya.

3. Trapesium Sama Kaki

Trapesium sama kaki merupakan trapesium yang mempunyai dua buah sisi yang sama panjangnya, sisi tersebut biasa di sebut dengan kaki.

Sifat-sifat Trapesium Sama Kaki

• Mempunyai dua buah sisi( kaki ) yang sama panjangnya dan dua buah sisi sejajar yang panjangnya berbeda. 
• Mempunyai dua buah sudut yang berdekatan yang besarnya sama.
• Mempunyai dua buah diagonal yang panjangnya sama.

Bagi teman-teman yang ingin mengetahui bagaimana rumus luas dan keliling dari trapesium, kalian bisa membacanya di halaman ini rumus luas dan keliling trapesium.

Demikian pembahasan mengenai jenis-jenis trapesium dan sifat-sifat masing-masing trapesium semoga bermanfaat bagi teman-teman semua.[]

Related Posts:

Tweet

Rumus Luas Dan Keliling Trapesium Lengkap

Rumus Luas Dan Keliling Trapesium Lengkap - Pada pembahasa sebelumnya telah di bahas mengenai sifat sifat bangun datar jajar genjang, dan pada pertemuan kali ini kita akan melakukan tentang pembahasan cara menghitung rumus luas dan keliling dari bangun datar trapesium. Apa itu sih trapesium ? Trapesium merupakan sebuah bangun datar dua dimensi yang di bentuk oleh empat buah rusuk yang dua di antaranya saling sejajar namun tidak sama panjang. Menurut wikipedia trapesium termasuk jenis bangun datar segi empat. Bangun trapesium di bagi dalam 3 jenis yakni trapesium sembarang, trapesium sama kaki dan trapesium siku-siku.

Rumus matematika pada pertemuan saat ini akan mencoba menjelaskan tentang rumus-rumus yang biasa di gunakan untuk menyelesaikan soal tentang bangun datar trapesium. Berikut ini merupakan pembahasan tentang rumus luas trapesium dan keliling trapesium lengkap beserta contoh soal dan pembahasannya. Silahkan kamu simak selengkapnya.

Rumus Luas Trapesium dan Rumus Keliling Trapesium

Untuk bisa menemukan berapa ukuran luas dan ukuran keliling sebuah bangun trapesium kita bisa menggunakan rumus berikut ini :

Gambar Trapesium 

Luas Trapesium =    1/2 x jumlah sisi sejajar x tinggi

Keterangan :

Jumlah sisi sejajar = AB + CD ( lihat gambar di atas  )

Tinggi =  t  ( DE ) ( lihat gambar  di atas )

Keliling Trapesium = AB + BC + CD +DA  

Keterangan :

Keliling trapesium merupakan jumlah seluruh sisi-sisinya

AB, BC, CD, DA adalah sisi-sisi trapesium

( Lihat gambar )

Contoh soal luas dan keliling trapesium dan pembahasannya :

1. Sebuah trapesium diketahui mempunyai panjang sisi-sisi sejajar masing-masing adalah 8 cm dan 20 cm dan ukuran tingginya 12 cm. Hitunglah berapa luas bangun trapesium ini ?

Penyelesaian:
Luas = ½ x ( Jumlah sisi sejajar ) x t
Luas = ½ x (8 cm + 20 cm) x 12 cm
Luas = ½ x 28 x 12
Luas = ½ x 336 cm
Luas = 168 cm²

Jadi luas bangun trapesium di atas adalah 168 cm²


Demikian penjelasan tentang Rumus Luas Dan Keliling Trapesium Lengkap semoga teman-teman semua bisa mendapatkan tambahan pengetahuan.[]

Related Posts:

Tweet

Sifat Sifat Jajar Genjang Lengkap

Sifat Sifat Jajar Genjang - Jajar genjang atau yang dalam bahasa inggris di sebut dengan parallelogram merupakan sebuah bangun datar dua dimensi yang terbentuk dari dua buah pasang sisi yang sama panjangnya serta sejajar. Untuk mengetahui bagaimana menghitung rumus jajar genjang anda bisa lihat disini rumus jajar genjang.

Ciri ciri jajar genjang :

1. Sisi-sisi yang berhadapan di setiap bangun jajar genjang selalu sama panjangnya serta sejajar.( Pada gambar diatas sisi PQ = SR dan QR = SP )
2. Sudut-sudut yang berhadapan di setiap bangun jajar genjang sama besarnya. ( Pada gambar diatas Sudut Q = sudut S dan Sudut P = sudut R )
3. Jumlah dua besar sudut yang berdekatan di setiap bangun jajar genjang adalah 180 derajat. 
4. Di setiap bangun jajar genjang kedua diagonal yang saling membagi dua sama panjangnya.
5. Memiliki simetri putar tingkat dua dan tidak mempunyai simetri lipat.
6. Memiliki dua buah sudut tumpul dan dua buah sudut lancip.
7. Jumlah semua sudut yang di miliki jajaran genjang adalah 360 derajat.

Demikian beberapa sifat-sifat bangun jajar genjang lengkap semoga bermanfaat bagi pembaca semua.[]

Related Posts:

Tweet

Rumus Luas Dan Keliling Jajar Genjang

Rumus luas dan keliling jajar genjang - Jajar genjang atau biasa di sebut juga dengan jajaran genjang ( parallelogram ) merupakan sebuah bangun datar dua dimensi yang terbentuk oleh dua buah pasang rusuk yang sama panjang dan sejajar dengan pasangannya, serta mempunyai dua buah pasang sudut yang masing-masing besarnya sama dengan sudut di depannya. Jajar genjang yang memiliki empat buah rusuk yang panjangnya sama disebut dengan bangun belah ketupat.

 Rumus Luas Jajar Genjang

Perhatikan gambar jajar genjang di atas, Untuk menghitung luas dari sebuah jajar genjang caranya sama dengan menghitung luas pada bangun persegi panjang ( lihat rumus persegi panjang ). Perbedaannya dalam pada jajaran genjang ukuran panjang menjadi alas (a) dan lebar menjadi tinggi (t). Sehingga rumus luas jajar genjang adalah :

L = alas x tinggi

Keterangan :
L adalah luas jajar genjang
alas merupakan panjang alas
tinggi merupakan panjang tinggi

Rumus Keliling Jajar Genjang

Selain mempunyai kesamaan dalam cara menghitung luas dengan bangun persegi panjang, untuk menghitung keliling dari sebuah jajar genjang caranya pun hampir sama dengan menghitung keliling pada persegi panjang yang dirumuskan sebagai berikut :

Perhatikan gambar di atas,

K = AB + BC + CD + AD

Keterangan :
K adalah keliling jajar genjang
AB, BC, CD, AD adalah panjang masing-masing sisinya

Karena panjang AB = CD dan panjang BC = AD, maka rumus keliling jajar genjang bisa di rumuskan sebagai berikut.

K = 2 x ( AB + BC )

atau bisa juga

K = 2 x alas + 2 x sisi miring

Dari ketiga cara di atas hasil yang akan di temukan pasti akan sama, jadi terserah anda mau memakai cara yang mana.

Mengapa prinsip pada jajar genjang hampir sama dengan bangun persegi panjang berikut ini penjelasannya.

Perhatikan gambar di atas dengan seksama, setelah bagian kiri dari jajar genjang di potong kemudian di gabungkan dengan bagian di sebelah kanan maka akan terbentuklah sebuah bangun datar persegi panjang, itulah mengapa prinsip menghitung luas dan keliling kedua bangun datar ini hampir sama.

Contoh Soal Jajar Genjang Dan Pembahasannya

1. Sebuah jajar genjang memiliki panjang alas 20 cm dan ukuran tinggi  10 cm. Hitunglah berapa luas bangun datar jajaran genjang tersebut?

Jawab :
diketahui a = 20 dan t = 10

maka :
Luas = Alas x Tinggi
Luas = 20 x 10 = 200 cm2

Jadi luas jajaran genjang tersebut adalah 200 cm2

2. Jika diketahui sebuah bangun jajar genjang mempunyai luas 300 cm2 dan memiliki alas 30 cm, hitunglah tinggi dari bangun jajar genjang di atas ?

Jawab :

Diketahui : L = 300 dan a = 30

maka :

L = alas x tinggi
300 = 30 x t
t   = 300/30
t   = 10 cm

Jadi ukuran tinggi jajar genjang di atas adalah 10 cm.

Demikian pembahasan tentang Rumus Luas Dan Keliling Jajar Genjang semoga bermanfaat bagi kita semua salam sukses.()

Related Posts:

Tweet

Sifat-Sifat Segitiga Sama Sisi

Segitiga sama sisi merupakan salah satu jenis segitiga jika di lihat dari panjang sisinya, termasuk juga segitiga sama kaki dan segitiga sembarang. ( Baca pembahasan sebelumnya mengenai sifat segitiga sama kaki dan segitiga sembarang )

Segitiga ini sangat gampang dan mudah untuk memahami sifat-sifatnya. Silahkan di simak selengkapnya sifat dan ciri segitiga sama sisi.

1. Memiliki tiga buah sisi yang panjangnya sama. ( Pada gambar yaitu panjang LK = ML = MK )

2. Memiliki tiga buah sudut yang besarnya sama. ( Pada gambar Sudut K = Sudut M = Sudut L yaitu 60⁰ hal ini berlaku karena jumlah semua sudut dari sebuah segitiga adalah 180 derajat )

3. Memiliki tiga buah simetri putar.

4. Memilki tiga buah simetri lipat.

Demikian pembahasan mengenai beberapa ciri atau sifat dari segitiga sama sisi semoga bermanfaat bagi teman-teman semua.[]

Related Posts:

Tweet

Sifat Sifat Segitiga Sembarang

Segitiga sembarang adalah salah satu jenis segitiga yang dilihat dari panjang sisi-sisinya sehingga boleh di bilang masih kerabat dekat dengan segitiga sama sisi dan sama kaki tetapi cirinya cukup berbeda. Oh iya jangan lupa baca juga pembahasan sebelumnya mengenai sifat segitiga sama kaki.

Agar lebih jelasnya silahkan di lihat sifat-sifat segitiga dibawah ini :

1. Mempunyai tiga buah sisi yang tidak sama panjangnya. ( pada gambar diatas ketiga sisi yang di maksud adalah Panjang BA ≠ CB ≠ AC ).

2. Tidak memliki simetri lipat.

3. Mempunyai simetri putar hanya satu buah.

4. Ketiga sudutnya mempunyai besar yang berbeda. ( Pada gambar bisa di lihat sudut C ≠ sudut A ≠ sudut B )

Demikian adalah ciri-ciri dari segitiga sembarang semoga bermanfaat bagi teman semua.[]

Related Posts:

Tweet

Sifat Sifat Segitiga Sama Kaki

Sifat Sifat Segitiga Sama Kaki - Setelah sebelumnya kami membahas tentang sifat-sifat segitiga siku-siku pada kesempatan kali ini kami akan mencoba berbagi mengenai sifat-sifat segitiga sama kaki. Segitiga sama kaki merupakan salah satu jenis segitiga yang dilihat berdasarkan panjang sisi-sisinya.

Berikut ini adalah beberapa sifat dan ciri-ciri yang dimiliki segitiga sama kaki.

1. Mempunyai dua buah sudut alas yang besarnya sama. ( Pada gambar terlihat di sudut Q dan sudut R )

2. Memiliki dua buah sisi yang sama panjangnya, sisi-sisi itu biasa di sebut dengan kaki segitiga. ( Pada gambar terlihat di sisi QP dan sisi PR )

3. Mempunyai satu buah sumbu simetri.

4. Dapat menempati bingkainya dengan dua cara.

Demikian beberapa ciri-ciri segitiga sama kaki semoga bermanfaat bagi pembaca semua.[]

Related Posts:

Tweet

Sifat-Sifat Segitiga Siku-Siku

Segitiga siku-siku merupakan salah satu jenis segitiga dilihat dari sudutnya. Segitiga jenis ini sangat mudah untuk di pahami ciri dan sifatnya. Berikut adalah beberapa sifat atau ciri segitiga ssiku-siku.

Segitiga siku-siku bisa terbentuk dari sebuah bangun persegi panjang, yaitu dengan cara menarik salah satu garis diagonal pada persegi panjang.

Ketika garis diagonal sudah terhubung maka akan terbentuklah dua buah segitiga siku siku yang sama besar dan sebangun atau kongruen.

Sebuah segitiga siku-siku memliki dua buah sisi siku-siku, yang dimana kedua sisi siku-siku tersebut mengapit sebuah sudut siku-siku dan 1 sisi miring atau hypotenusa.

Baca juga pembahasan rumus segitiga siku-siku.

Perhatikan gambar segitiga ABC di atas, dari gambar tersebut kita bisa melihat jika segitiga siku-siku mempunyai ciri-ciri:

1. Segitiga siku-siku memiliki dua buah sisi siku-siku, yang dimana kedua sisi siku-siku tersebut mengapit sebuah sudut siku-siku dan 1 sisi miring atau hypotenusa.

2. Hypotenusa atau sisi miring di setiap segitiga siku-siku selalu terletak di depan sudut siku-siku.

3. Memiliki satu buah sudut yang besarnya 90 derajat.

Itulah beberapa ciri atau sifat dari segitiga siku-siku semoga bermanfaat.[]

Related Posts:

Tweet

Sifat Sifat Segitiga

a. Ketidaksamaan pada segitiga

Pada suatu bangun datar segitiga, sudut terbesar yang di miliki selalu berhadapan dengan sisi yang mempunyai ukuran terpanjang dan sisi dengan ukuran paling pendek selalu berhadapan dengan sudut yang terkecil.

b. Sifat-sifat segitiga sama kaki

• Mempunyai satu buah sumbu simetri dan dapat menempati bingkainya dengan pas dengan dua cara.
• Memiliki dua buah sisi yang sama panjang dan juga memiliki dua buah sudut yang sama besarnya.

c. Sifat-sifat segitiga sama sisi

• Mempunyai tiga buah sumbu simetri putar tingkat tiga serta bisa menempati bingkainya dengan tepat dengan enam cara.
• Mempunyai tiga buah sisi yang sama panjang.
• Mempunyai tiga buah sudut yang sama besar.

d. Segitiga siku-siku

• Memiliki sisi tegak, sisi datar dan sisi miring.
• Mempunyai sudut siku-siku  ( 90° )
• hypotenusa atau sisi miring pada segitiga siku-siku selalu terletak di depan sudut siku-siku.

e. Segitiga sembarang

• Ketiga sisi yang di milikinya panjangnya tidak sama.
• Ketiga sudut yang dimilikinya tidak sama besar.

f. Jumlah ketiga sudut pada sebuah segitiga berjumlah 180 derajat.
g. Mempunyai tiga buat sudut  dan tiga buah sisi.

Related Posts:

Tweet

Pengertian Persamaan Garis Lurus dan Cara Menggambarnya

Pengertian Persamaan Garis Lurus - Persamaan garis lurus juga dapat disebut sebagai persamaan linear. persamaan linear ada yang terdiri dari satu variabel dan ada juga yang terdiri dari dua variabel. Karena Rumus Matematika Dasar sudah pernah memberikan penjelasan mengenai Persamaan Linear Satu Variabel dan Persamaan Linear Dua Variabel maka postingan kali ini akan difokuskan kepada pembahasan mengenai persamaan garis lurus dan langkah-langkah untuk menggambarnya. 

Pengertian dan Cara Menggambar Persamaan Garis Lurus

Secara sederhana persamaan garis lurus dapat didefinisikan sebagai sebuah garis lurus dimana posisinya ditentukan oleh sebuah persamaan dan apabila persamaan tersebut digambarkan pada bidang cartesius maka akan menghasilkan sebah garis yang lurus. Salah satu contoh persamaan yang menghasilkan garis lurus adalah x + y = 3. Bagaimana kita bisa mengetahui bahwa persamaan tersebut dapat menghasilkan garis lurus? mari langsung saja kita buktukan dengan cara berikut ini:

Salah satu cara yang bisa kita lakukan untuk membuktikan persamaan garis lurus adalah dengan menggambarkan garis lurus ke dalam bidang cartesius dengan menggunakan koordinat yang dihasilkan dari persamaan tersebut, contohnya:

Kita misalkan x = 0, maka:

x + y = 3

0 + y = 3

y = 3

titik pertama yang kita peroleh adalah koordinat (0, 3)

Kita misalkan x = 1, maka:

x + y = 3

1 + y = 3

y = 2

titik kedua yang kita peroleh adalah koordinat (1, 2)

Kita misalkan x = 2, maka:

x + y = 3

2 + y = 3

y = 1

titik ketiga yang kita peroleh adalah koordinat (2, 1)

Kita misalkan x = 3, maka:

x + y = 3

3 + y = 3

y = 0

titik kedua yang kita peroleh adalah koordinat (3, 0)

Setelah kita menemukan koodinatnya, tinggal kita masukkan saja ke dalam bidang cartesius, sehingga hasilnya menjadi seperti ini:

Dari gambar di atas kita dapat melihat bahwa ketika kita menarik garis diantara titik-titik koordinat yang diperoleh, maka akan dihasilkan sebuah garis yang lurus. Itu artinya kita dapat menyimpulkan bahwa persamaan x + y = 3 terbukti sebagai sebuah persamaan garis lurus.

Bagaimana? Apakah kalian sudah mengerti dan paham tentang pengertian persamaan garis lurus dan cara menggambarnya? Jika kalian mengamati penjelasan di atas dengan baik, tidaklah sulit untuk bisa memahami apa itu persamaan garis lurus serta bagaimana cara menggambarkannya ke dalam koordinat cartesius. Semoga penjelasan materi ini bermanfaat untuk kalian semua.

Related Posts:

Tweet

Jenis-Jenis Segitiga Lengkap

Jenis-Jenis Segitiga - Segitiga adalah sebuah bidang datar yang terbentuk oleh tiga buah garis yang saling berpotongan atau sebuah bidang datar yang dibatasi oleh tiga buah garis yang memiliki tiga buah sudut.

Jenis-jenis segitiga ada beberapa macam, yang dikelompokkan berdasarkan ciri-ciri khususnya seperti berdasar sudutnya, berdasar panjang sisinya dan berdasar sudut serta panjang sisinya. Mari kita bahas satu persatu.

1. Jenis-Jenis Segitiga Dilihat Dari Panjang Sisi-Sisinya

Di lihat dari panjang sisi-sisinya segitiga di bedakan menjadi tiga macam yaitu :

a. Segitiga sama sisi

Segitiga sama sisi adalah segitiga yang mempunyai tiga sisi sama panjang dan semua sudutnya sama besarnya yaitu 60⁰.

Perhatikan gambar segitiga sama sisi KLM di atas,

• Panjang KL = LM = KM
• Sudut K = Sudut M = Sudut L ( yaitu 60⁰ )

b. Segitiga sama kaki

Segitiga sama kaki adalah segitiga dengan dua sisinya yang sama panjang dan terbentuk dari dua segitiga siku-siku yang kongruen.

Perhatikan gambar segitiga sama kaki di atas,

• Panjang PQ = PR ( PQ dan PR di sebut kaki ).
• Sudut Q = Sudut R ( di sebut sudut-sudut kaki segitiga PQR ).
• Sisi QR merupakan alas dan Sudut P adalah sudut puncak.

c. Segitiga sembarang

Segitiga sembarang adalah segitiga dengan ketiga sisinya tidak sama panjang dan juga sudut-sudutnya tidak sama besar.

Perhatikan segitiga sembarang ABC di atas ,

• Panjang AB ≠ BC ≠ CA.
• sudut A ≠ sudut B ≠ sudut C.

2. Jenis-Jenis Segitiga Dilihat Dari Besar Sudut-Sudutnya

 Dilihat dari besar sudut-sudutnya jenis segitiga di bedakan dalam tiga jenis yaitu :

a. Segitiga lancip

Segitiga yang memiliki tiga buah sudutnya berbentuk lancip dimana besar masing-masing sudutnya lebih dari 0⁰ dan kurang dari 90⁰ disebut dengan segtitiga lancip.

Perhatikan gambar segitiga lancip ABC di atas,

• Sudut A, sudut B dan Sudut C merupakan sudut lancip.

b. Segitiga siku-siku

Segitiga dengan salah satu sudutnya berukuran 90⁰ disenut dengan segitiga siku-siku.

Perhatikan gambar segitiga siku-siku ABC di atas,

• Sudut A merupakan sudut siku-siku yang ukurannya adalah 90^0.

c. Segitiga tumpul

Segitiga yang salah satu sudutnya tumpul dimana salah satu sudutnya lebih dari 90⁰ tetapi kurang dari 180⁰ di sebut dengan segitiga tumpul.

Perhatikan gambar segitiga tumpul PQR di atas,

• Sudut P merupakan sudut tumpul dari segitiga tersebut.

3. Jenis-Jenis Segitiga Dilihat Dari Panjang Sisi-Sisinya Dan Besar Sudut-Sudutnya

Dilihat dari panjang sisi-sisinya dan besar sudut-sudutnya segitiga di bedakan dalam tiga jenis yaitu :

a. Segitiga siku-siku sama kaki

Segitiga yang memiliki besar salah satu sudutnya 90⁰ dan kedua sisinya sama panjang biasa di sebut dengan segitiga siku-siku sama kaki.

b. Segitiga lancip sama kaki

Segitiga dengan sudut lancip dan kedua sisinya sama panjang di sebut dengan segitiga lancip sama kaki.

c. Segitiga tumpul sama kaki

Segitiga yang mempunyai salah satu sudutnya tumpul dan memiliki dua sisi yang sama panjangnya.

Tahukah kamu jika di jumlah tiga sudut pada sebuah segitiga adalah 180⁰, selain itu tahukah kamu garis-garis istimewa yang dimiliki segitiga. Demikian pembahasan mengenai jenis-jenis segitiga semoga bermanfaat bagi teman-teman semua.[]

Related Posts:

Tweet

Rumus Segitiga Sama Sisi

Pengertian segitiga sama sisi

Rumus Segitiga Sama Sisi - Segitiga sama sisi merupakan salah satu jenis segitiga yang dilihat dari panjang sisinya, dinamakan segitiga sama sisi di karenakan ketiga sisinya sama panjang.
Gambar di atas merupakan gambar segitiga XYZ yang panjang ketiga sisinya sama.

Segitiga sama sisi mempunyai sifat-sifat :

1. Memiliki tiga buah sisi yang sama panjang.
2. Memiliki tiga buah sudut yang sama besar.
3. Memiliki tiga buah sumbu simetri.

Rumus luas segitiga sama sisi :

Kita mengetahui jika rumus umum dari sebuah segitiga adalah L = ½ a x t
Nah pada segitiga sama sisi untuk menghitung luasnya selain menggunakan rumus diatas juga bisa menggunakan rumus cepat untuk mencari luasnya yaitu :
L = a²/4 x √3

dimana a merupakan panjang sisi segitiga.

Rumus keliling segitiga sama sisi :

Untuk menghitung kelilingnya saya rasa tidak ada perbedaan dengan menghitung keliling sebuah segitiga pada umumnya.

Rumusnya yaitu : K = sisi 1 + sisi 2 +sisi 3
Atau bisa juga dengan cara K = panjang sisi x 3
hal tersebut bisa terjadi karena panjang semua sisinya sama.

Jangan lupa baca juga pembahasan mengenai Segitiga Siku-siku dan Segitiga Sama kaki.

Demikian pembahasan mengenai segitiga sama sisi semoga bermanfaat.[]

Related Posts:

Tweet

Rumus Segitiga Sama kaki

Rumus Segitiga Sama kaki - Segitiga sama kaki mempunyai pengertian sebuah segitiga yang mempunyai dua sisi yang sama panjang dan dua sudut yang sama besar yaitu sudut yang berhadapan dengan sisi yang panjangnya sama.

Segitiga sama kaki dibentuk dari 2 buah segitiga siku siku yang kongruen yakni dengan cara menghimpitkan kedua sisi yang panjangnya sama.

Baca juga artikel sebelumnya tentang Rumus Segitiga Siku-siku.

gambar segitiga sama kaki

Perhatikan gambar di atas. Segitiga ADC dan segitiga BDC adalah 2 buah segitiga siku siku yang kongruen. Sisi CD adalah sisi siku siku yang sama panjangnya dari kedua segitiga siku siku diatas. Jadi bisa kita peroleh kesimpulan bahwa segitiga ABC adalah sebuah segitiga sama kaki dengan sisi AC=BC yang sama panjangnya sebagai kaki dari segitiga tersebut.

Segitiga sama kaki mempunyai sifat-sifat antara lain :

1. Memiliki 2 buah sisi yang sama panjangnya sebagai kaki dari segitiga
2. Memiliki 1 sumbu simetri
3. Memiliki 2 buah sudut yang besarnya sama yakni sudut-sudut yang berhadapan dengan sisi yang sama panjang.
4. Segitiga sama kaki adalah salah satu bangun lipat simetri yang bisa menempati bingkainya dengan dua macam cara.

Rumus segitiga sama kaki :

Segitiga adalah bagian salah satu dari bangun datar yang mempunyai keliling dan
luas.
Untuk menghitung Keliling segitiga sama kaki di gunakan rumus :
K = sisi 1 + sisi 2 +sisi 3
Jadi untuk mencari keliling segitiga sama kaki dengan menjumlahkan semua panjang sisi-sisinya( pada dasarnya hal ini sama dengan semua rumus keliling segitiga )

Untuk menghitung Luas segitiga sama kaki di gunakan rumus :
L = ½ a x t
dimana L adalah luas, a adalah panjang alas dan t adalah tinggi dari segitiga tersebut.

Contoh soal segitiga sama kaki dan pembahasannya :

1. Jika di ketahui sebuah segitiga sama kaki panjang alasnya 12 cm sedangkan panjang kakinya 10 cm. Hitunglah luas dan keliling segitiga tersebut !

Jawab :

Diketahui :
a = 12 cm
s = 10 cm
ditanya :
a. K . . . . ?
b. L . . . . ?

Jawab :

a. Keliling segitiga
K= sisi 1 + sisi 2 + sisi 3
K = 12 cm+ 10 cm + 10 cm
K = 32 cm

b. Luas segitiga

Coba kamu perhatikan gambar segitiga segitiga sama kaki di bawah ini.

aC adalah tinggi segitiga, untuk mencari tinggi sebuah segitiga siku-siku kita bisa menggunakan persamaan phytagoras. Jika alasnya adalah 12 cm maka panjang aB = 6 cm

aC2 = BC2 - aB2
aC2 = 102 – 62
aC2 = 100 –  36
aC2 = 64
aC = 8 cm
jadi tinggi segitiga tersebut = 8 cm

Luas segitiga = ½ x a x t
L = ½ x 12 x 8
L = 48 cm2
Jadi keliling segitiga sama kaki tersebut 32 cm sedangkan luanya 48 cm2.

2. Jika diketahui luas segitiga 48 cm2. Hitung tinggi segitiga jika alasnya 12 cm !
Diketahui :

L = 48 cm2
a = 12 cm

ditanya :
t . . . . ?

jawab :

L = ½ x a x t
48 = ½ x 12 x t
48/0,5 = 12 x t
96 = 12 x t
96/12 = t
8 cm = t
Jadi tinggi segitiga tersebut 8 cm.

Demikian pembahasan tentang Rumus Segitiga Sama kaki semoga bermanfaat bagi kita semua salam sukses.()

Related Posts:

Tweet

Rumus Segitiga Siku-siku

Apa itu pengertian segitiga siku-siku

Gambar  segitiga siku siku

Segitiga siku-siku adalah sebuah segitiga yang salah satu dari tiga sudutnya mempunyai sudut 90⁰ atau siku-siku, seperti yang bisa kamu lihat pada gambar di atas.
Pada gambar diatas pada titik C sudut siki-siku dari segitiga tersebut.

Rumus-rumus segitiga siku-siku

a. Jika panjang sisi a dan panjang sisi b sudah diketahui ukurannya maka panjang sisi c dapat ditentukan dengan persamaan c²= a² + b²

b. Jika panjang sisi a dan panjang sisi c sudah diketahui ukurannya maka panjang sisi b dapat ditentukan dengan persamaan b² = c² – a²

c. Jika panjang sisi b dan panjang sisi c sudah diketahui ukurannya maka panjang sisi a dapat ditentukan dengan persamaan a² = c² – b²

Persamaan di atas biasa di sebut dengan teorema phytagoras.( lihat rumus pythagoras )

Sedangkan untuk menghitung keliling segitiga siku-siku dapat digunakan rumus :
K = sisi a + sisi b + sisi c, atau
K = sisi + sisi + sisi

Dan untuk luas segitiga siku-siku dapat di gunakan persamaan :
L = ½ x alas x tinggi
L = ½ x a x t

Contoh soal segitiga siku-siku dan pembahasannya

1.  Sebuah segitiga ABC adalah segitiga siku-siku dengan sudut siku-sikunya berada di titik A. Hitung panjang BC, jika panjang AB 8 cm
dan panjang AC 6 cm !
Jawab :

Diketahui :
AB = 8 cm
AC = 6 cm

Ditanya :
BC . . . . ?

Jawab :
BC² = AB² + AC²
BC² = 8² + 6²
BC² = 64 + 36
BC² = 100
BC = 10 cm
Jadi panjang sisi BC adalah 10 cm

2. Perhatikan gambar segitiga di atas , jika panjang sisi c = 5 cm dan panjang sisi a =  3 cm, hitunglah panjang sisi b !

Diketahui :
c = 5 cm
a = 3 cm

ditanya :
b . . . ?

jawab :
b² = c² - a²
b² = 5² – 3²
b² = 25 – 9
b² = 16
b = 4 cm
jadi panjang sisi b adalah 4 cm

3. Jika diketahui tinggi segitiga 4 cm dan alasnya 6 cm, hitunglah luasnya !

Diketahui :
t = 4 cm
a = 6 cm

ditanya :
L . . . .?

Jawab :
L = ½ x a x t
L = ½ x 6 cm x 4 cm
L = 12 cm²
Jadi luas segitiga adalah 12 cm²

4. Hitunglah keliling segitiga jika panjang sisi-sisinya 5 cm, 3 cm dan 4 cm !

Diketahui :
Misalkan
Sisi a = 5 cm
Sisi b = 4 cm
Sisi c = 3 cm

Ditanya :
K . . . . ?

Jawab :
K = sisi a + sisi b + sisi c
K = 5 cm + 4 cm + 3 cm
K = 12 cm
Jadi keliling segitiga tersebut adalah 12 cm.

Demikian pembahasan tentang Rumus Segitiga Siku-siku semoga bermanfaat bagi kita semua salam sukses.()

Related Posts:

Tweet

Pengertian Notasi Himpunan dan Anggota Himpunan

Notasi Himpunan dan Anggota Himpunan - Di dalam beberapa postingan sebelumnya Rumus Matematika Dasar pernah memberikan materi seputar Pengertian Himpunan. Untuk postingan kali ini materi yang dibahas masih berkaitan dengan pembahasan seputar himpunan yaitu pengertian notasi dan anggota himpunan. Kalian pastinya sudah mengetahui bahwa di dalam matematika biasanya suatu himpunan dinyatakan dengan menggunakan huruf kapital seperti A, B, C, D, E, F, ... dst. Adapun objek atau hal-hal lain yang terdapat di dalam himpunan tersebut dituliskan diantara kurung kurawal {....} dan tiap-tiap objek itu dipisahkan dengan menggunakan koma, contohnya adalah:

- A merupakan himpunan bilangan ganjil dari yang lebih kecil dari 15, 

   maka A = {1, 3, 5, 7, 9, 11, 13}

- B merupakan himpunan bilangan genap antara 1 dan 13 

   maka B = {2, 4, 6, 8, 10, 12}

Tiap-tiap objek ataupun benda yang berada di dalam kurung kurawal adalah anggota dari himpunan tersebut. Anggota himpunan biasa disebut juga sebagai elemen yang dinotasikan dengan lambang ∈. Sedangkan objek-objek ataupun benda yang tidak termasuk kedalam suatu himpunan dapat dianggap bukan anggota dari himpunan tersebut dan biasanya dinotasikan dengan lambang ∉.

Jumlah anggota dari suatu himpunan basanya dinyatakan sebagai n. Apabila C = {2, 3, 5, 6, 7, 8, 9, 11} maka banyaknya anggota himpunan B dituliskan sebagai n(C) = 8.

Di dalam matematika, himpunan bilangan tertentu biasanya dilambangkan atau dinotasikan dengan menggunakan huruf kapital tertentu, contohnya:

Contoh soal Notasi dan Anggota Himpunan

a. A adalah himpunan hewan laut.

b. K adalah hmpunan bilangan cacah yang kurang dari 10

c. M adalah himpunan nama bulan yang diawali dengan huruf J.

Jawab:

a. Anggota himpunan hewan laut adalah ikan, gurita, cumi-cumi, kerang, dst. Maka, A = {ikan, gurita, cumi-cumi, kerang,... dsb.}

b. Anggota himpunan bilangan cacah yang kurang dari 10 adalah 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Maka, K = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

c. Anggota himpunan nama bulan yang diawali dengan huruf J adalah Januari, Juni, dan Juli. Maka, M = {Januari, Juni, Juli}

Itulah sedikit penjelasan materi mengenai Pengertian Notasi Himpunan dan Anggota Himpunan. Semoga bermanfaat dan semoga kalian bisa menyerap materi tersebut dengan baik. Ikuti terus postingan Rumus Matematika Dasar untuk terus engasah kemampuan dan pengetahuan kalian mengenai pelajaran matematika. Sampai jumpa dan terima kasih.

Related Posts:

Tweet

Pengertian Gabungan Dua Himpunan dan Cara Menentukannya

Pengertian Gabungan Dua Himpunan - Ada cukup banyak materi yang berkaitan dengan himpunan diajarkan pada bangku sekolah menengah pertama. Salah satu diantaranya adalah mengenai gabungan dua himpunan. Tahukah kalian apa yang dimaksud sebagai gabungan dari dua himpunan? ada baiknya bila kalian membaca lagi materi Rumus Matematika Dasar yang membahas tentang Pengertian, Teori, Konsep Dan Jenis Himpunan Matematika jika kalian sudah memahami dengan baik apa itu yang disebut dengan himpunan maka kalian pastinya akan lebih mudah dalam memahami materi yang akan di bahas pada artikel ini. Sebelum kita beranjak lebih jauh ke dalam pembahasan materi, sebaiknya kalian amati terlebih dahulu contoh uraian berikut ini:

Pak Sukirlan pergi ke pasar untuk membeli beberapa jenis buah. Setelah berbelanja Pak Sukirlan kemudian pulang ke rumah dengan membawa dua buah keranjang. Keranjang pertama di isi dengan buah kelengkeng, duku, dan rambutan. Sementara keranjang yang kedua di isi dengan buah jambu, markisa, dan rambutan. Setibanya di rumah, buah-buahan tersebut di satukan ke dalam sebuah keranjang besar sehingga keranjang besar tersebut kini berisi gabungan buah-buahan yang dibeli oleh pak Sukirlan yaitu kelengkeng, duku, rambutan, jambu, dan markisa.

Dari contoh uraian di atas, kita dapat menyimpulkan bahwa apabila kedua keranjang yang dibawa oleh pak Sukirlan adalah himpunan A dan B. maka, gabungan dari himpunan A dan B adalah himpunan yang anggotanya merupakan anggota-anggota yang ada di himpunan A atau anggota-anggota yang ada di himpunan B. atau di dalam matematika dapat dituliskan menjadi:

A ∪ B = A union B (A gabungan B)

Cara Menentukan Gabungan Dua Himpunan

1. Himpunan Bagian

apabila A ⊂ C maka A ∪ B = B

Artinya, apabila anggota himpunan A termasuk ke dalam anggota himpunan B ( A adalah himpunan bagian dari B) maka gabungan dari kedua himpunan tersebut berisi seluruh anggota himpunan B.

2. Kedua Himpunan Beranggotakan Sama

apabila A = B maka A ∪ B = A = B

Artinya apabila anggota himpunan A sama persis dengan anggota himpunan B, maka gabungan dari kedua himpunan tersebut berisi anggota himpunan A atau B.

3. Himpunan tidak saling lepas

Sebagai contoh A = { 2, 3, 4, 6, 8} dan B = {2, 5, 6, 9} maka A U B = {2, 3, 4, 5, 6, 8, 9}

Banyaknya jumlah anggota dari gabungan dua himpunan dapat ditentukan dengan menggunakan rumus di bawah ini:

n(A ∪ B) = n(A) + n(B) - n(A ∩ B)

Contoh Soal:

Diketahui:

X = {1, 2, 3, 4, 6, 8}
Y = {2, 4, 5, 6, 9, 11}

Tentukanlah:

a.  anggota X ∩ Y
b. anggota X ∪ Y
c. n(X ∪ Y)


Jawab:

a. X ∩ Y = {2, 4, 6}
b. X ∪ Y = {1, 2, 3, 4, 5, 6, 8, 9, 11}
c. n(X ∪ Y)
n(X ∪ Y) = n(X) + n(Y) - n(X ∩ Y)
n(X ∪ Y) = 6 + 6 - 3
n(X ∪ Y) = 9


Sekian penjelasan dan contoh soal mengenai Pengertian Gabungan Dua Himpunan dan Cara Menentukannya semoga dapat membantu kalian untuk memahami lebih jauh materi mengenai himpunan. Sampai berjumpa pada pembahasan materi pelajaran matematika selanjutnya.

Related Posts:

Tweet