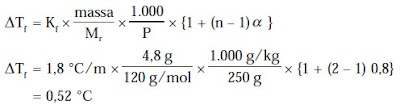Rangkuman Materi Sifat Koligatif Larutan

Rangkuman Materi Sifat Koligatif Larutan - Berikut ini RumusKimia.net akan share Rangkuman Materi Sifat Koligatif Larutan. Rangkuman materi ini merupakan garis besar dari pembahasan yang telah kami share sebelumnya sehingga dapat sahabat jadikan sebagai pengingat kembali materi yang telah sahabat pelajari sebelumnya. Tapi jika sahabat membutuhkan penjelasan dari setiap materi khusus dalam pembahasan utama Sifat Koligatif Larutan, sahabat dapat mempelajarinya kembali materi per materi.

Rangkuman Materi Sifat Koligatif Larutan

Baca juga: Tata Nama Eter Dilengkapi Contoh Penamaanya.

Rangkuman Materi Sifat Koligatif Larutan

Berikut rangkuman materinya:

1. Molalitas

Molalitas adalah besaran yang berguna untuk menghitung jumlah zat terlarut yang dinyatakan dalam mol dan jumlah pelarut dalam kilogram.

[Lihat Selengkapnya: Rumus Perhitungan Molalitas dan Contoh Soal Jawab.]

2. Fraksi mol

Fraksi mol merupakan satuan konsentrasi yang semua komponen larutannya dinyatakan berdasarkan mol. Total fraksi mol = 1

[Lihat Selengkapnya: Fraksi Mol Beserta Contoh Soal dan Penyelesaian.]

3. Sifat koligatif larutan nonElektrolit

Sifat koligatif bergantung pada jumlah zat yang terlarut pada larutan. Sifat koligatif terdiri atas penurunan tekanan uap (ΔP), kenaikan titik didih (ΔT_b) dan penurunan titik beku (ΔT_f), dan tekanan osmotik.

a. Penurunan tekanan uap (ΔP)

b. Kenaikan titik didih (ΔT_b)

ΔT_b= K_b × m atau ΔT_b = T_b – T_b^o

c. Penurunan titik beku (ΔT_f)

ΔT_f = K_f × m atau ΔT_f = T_f^o – T_f

d. Tekanan osmotik (π)

π = MRT

[Lihat Selengkapnya:

• Penurunan Tekanan Uap Sifat Koligatif Larutan Nonelektrolit.
• Kenaikan Titik Didih Sifat Koligatif Larutan Nonelektrolit.
• Penurunan Titik Beku Sifat Koligatif Larutan Nonelektrolit.
• Tekanan Osmotik Larutan Nonelektrolit.]

4. Sifat koligatif larutan elektrolit

Sifat koligatif larutan elektrolit bergantung pada bilangan faktor Van’t Haff. Jadi, perhitungan penurunan tekanan uap, kenaikan titik didih, dan tekanan osmotik dikalikan dengan faktor Van’t Hoff (i).

i = 1 + (n – 1)α

a. Penurunan tekanan uap jenuh

ΔP = x_BP° {1 + (n – 1) α}

b. Kenaikan titik didih

ΔT_b = K_b.m.i  atau ΔT_b = K_b.m.{1 + (n – 1) α}

c. Penurunan titik beku

ΔT_f  = K_f .m.i  atau ΔT_f  = K_f.m.{1 + (n – 1) α}

d. Tekanan osmotik

π = MRT.i   atau  π = MRT {1 + (n – 1) α}

[Lihat Selengkapnya:

• Sifat Koligatif Larutan Elektrolit.
• Rumus dan Contoh Soal Penurunan Tekanan Uap Jenuh, Kenaikan Titik Didih, dan Penurunan Titik Beku Larutan Elektrolit.
• Rumus dan Contoh Soal Tekanan Osmotik Larutan Elektrolit.]

Demikian Rangkuman Materi Sifat Koligatif Larutan yang dapat kami rangkum pada kesempatan kali ini, dan nantikan rangkuman materi kimia lainnya hanya di RumusKimia.net.

Pustaka:

[Kimia Kelas 12 IPA oleh Iman Rahayu 2009]

[Rumus Kimia]

Related Posts:

Tweet

Rumus dan Contoh Soal Tekanan Osmotik Larutan Elektrolit

Rumus dan Contoh Soal Tekanan Osmotik Larutan Elektrolit - Dalam materi sifat koligatif larutan elektrolit, selain penurunan tekanan uap jenuh serta kenaikan titik didih dan penurunan titik didih, juga dikenal tekanan osmotik larutan elektrolit.

Rumus dan Contoh Soal Tekanan Osmotik Larutan Elektrolit

Lihat juga:

• Rumus dan Contoh Soal Penurunan Tekanan Uap Jenuh, Kenaikan Titik Didih, dan Penurunan Titik Beku Larutan Elektrolit.
• Tata Nama Eter.

Rumus dan Contoh Soal Tekanan Osmotik Larutan Elektrolit

Pada kesempatan ini RumusKimia.net akan membahas materi khusus Rumus dan Contoh Soal Tekanan Osmotik Larutan Elektrolit. Untuk mengetahui tekanan osmotik melalui persamaan atau rumus yang berlaku, tetap dihubungkan dengan faktor van't Hoff. Tekanan osmotik untuk larutan elektrolit diturunkan dengan mengalikan faktor van't Hoff [lihat Sifat Koligatif Larutan Elektrolit]. Berikut persamaannya:

π = MRT {1 + (n – 1) α }

Keterangan:

• π = Tekanan osmotik (atm)
• R = Tetapan Gas (0,082 L atm/mol K)
• T = Suhu absolut larutan (K)
• M = molaritas larutan (mol/L)]
• n = jumlah ion dari elektrolit
• α = derajat ionisasi elektrolit

Catatan:

1. Jika diketahui suhu bukan dalam derajat Kelvin, maka di ubah satuannya menjadi derajat Kelvin.
2. Untuk penentuan [M = molaritas larutan (mol/L)] digunakan persamaan:

[Untuk lebih jelasnya mengenai Molaritas, Lihat Perhitungan Molalitas]

Perhatikanlah contoh-contoh soal berikut ini:

Contoh Soal 1

Sebanyak 5,85 gram NaCl (Mr = 58,5 g/mol) dilarutkan dalam air sampai volume 500 mL. Hitunglah tekanan osmotik larutan yang terbentuk jika diukur pada suhu 27 °C dan R = 0,082 L atm/mol K.

Jawab:

diketahui, NaCl (n = 2) dan α = 1

π = MRT {1 + (n – 1)α }

 = 9,84 atm

Jadi, tekanan osmotik larutan tersebut adalah 9,84 atm.

Contoh Soal 2

Sebanyak 38 g elektrolit biner (Mr = 95 g/mol) dilarutkan dalam air sampai dengan volume 1 L pada suhu 27 °C dan memiliki tekanan osmotik 10 atm. Hitunglah derajat ionisasi elektrolit biner tersebut.

Jawab:

π = M R T {1 + (n – 1)α }

α = 0,016

Jadi, derajat ionisasi larutan tersebut adalah 0,016.

Contoh Soal Pilihan Ganda Analisis

Jika diketahui tekanan osmotik larutan 10 gram asam benzoat, C₆H₅COOH, dalam benzena adalah 2 atm pada suhu tertentu, larutan 20 gram senyawa binernya (C₆H₅COOH)₂ dalam pelarut yang sama memiliki tekanan osmotik sebesar....

A. 0,5 atm

B. 1,0 atm

C. 2,0 atm

D. 4,0 atm

E. 8,0 atm

Pembahasan:

Oleh karena perbandingan massa / Mr sama, molaritas akan sama dan tekanan osmotik pun sama. Jadi, tekanan osmotiknya sebesar (A) 2 atm.

Nach demikian share materi kimia kali ini mengenai Rumus dan Contoh Soal Tekanan Osmotik Larutan Elektrolit. Semoga materi kimia di atas dapat memberikan manfaat bagi kita semua. Mohon saran dari sahabat dalam pengembangan materi kimia kali ini dan selanjutnya.

Pustaka:

[Rumus Kimia]

[Kimia Kelas 12 IPA by Iman Rahayu]

[Google Images]

Related Posts:

Tweet

Rumus dan Contoh Soal Penurunan Tekanan Uap Jenuh, Kenaikan Titik Didih, dan Penurunan Titik Beku Larutan Elektrolit

Rumus dan Contoh Soal Penurunan Tekanan Uap Jenuh, Kenaikan Titik Didih, dan Penurunan Titik Beku Larutan Elektrolit - Sahabat RumusKimia.net, kali ini kami akan share kepada sahabat bagaimana rumus dan contoh soal penurunan tekanan uap jenuh, kenaikan titik didih, dan penurunan titik beku khusus untuk larutan elektrolit.

Rumus dan Contoh Soal Penurunan Tekanan Uap Jenuh, Kenaikan Titik Didih, dan Penurunan Titik Beku Larutan Elektrolit

Sebagaimana kita ketahui bersama bahwa hubungan sifat koligatif larutan elektrolit dan konsentrasi larutan dirumuskan oleh Van’t Hoff, yaitu dengan mengalikan rumus yang ada dengan bilangan faktor Van’t Hoff yang merupakan faktor penambahan jumlah partikel dalam larutan elektrolit.

Baca juga:

• Tata Nama Eter Dilengkapi Contoh Penamaanya.
• Sifat Koligatif Larutan Elektrolit.

Rumus dan Contoh Soal Penurunan Tekanan Uap Jenuh, Kenaikan Titik Didih, dan Penurunan Titik Beku Larutan Elektrolit

Untuk lebih jelasnya dari rumus dan contoh soalnya, berikut ulasannya khusus sahabat:

1) Rumus dan Contoh Soal Penurunan Tekanan Uap Jenuh

Rumus penurunan tekanan uap jenuh dengan memakai faktor Van’t Hoff hanya berlaku untuk fraksi mol zat terlarutnya saja (zat elektrolit yang mengalami ionisasi), sedangkan pelarut air tidak terionisasi. Oleh karena itu, rumus penurunan tekanan uap jenuh untuk zat elektrolit adalah:

ΔP = x_BP° {1 + (n – 1)α }

Perhatikanlah contoh soal penerapan rumus tekanan uap untuk zat elektrolit

berikut.

Contoh Soal

Hitunglah tekanan uap larutan NaOH 0,2 mol dalam 90 gram air jika tekanan uap air pada suhu tertentu adalah 100 mmHg!

Jawab:

Karena NaOH merupakan elektrolit kuat (α = 1) dan n = 2 maka

ΔP = x_BP° {1 + (n – 1)α }

      = 100 × 0,038 {1 + (2 – 1)1}

      = 7,6 mmHg

Tekanan uap larutan = 100 mmHg – 7,6 mmHg

                                 = 92,4 mmHg

Jadi, tekanan uap larutan NaOH adalah 92,4 mmHg.

2) Rumus dan Contoh Soal Kenaikan Titik Didih, dan Penurunan Titik Beku Larutan Elektrolit 

Seperti halnya penurunan tekanan uap jenuh, rumus untuk kenaikan titik didih dan penurunan titik beku untuk larutan elektrolit juga dikalikan dengan faktor Van't Hoff.

Contoh Soal

Perhatikanlah contoh-contoh soal berikut.

Sebanyak 4,8 gram magnesium sulfat, MgSO₄ (Mr = 120 g/mol) dilarutkan dalam 250 g air. Larutan ini mendidih pada suhu 100,15 °C. Jika diketahui K_b air 0,52 °C/m, K_f air = 1,8 °C/m, tentukan:

a. derajat ionisasi MgSO₄;

b. titik beku larutan.

Jawab:

a. Reaksi ionisasi MgSO₄ adalah MgSO_4(s) → Mg²⁺_(aq) + SO₄^2-_(aq)       (n = 2)

Kenaikan titik didih:

ΔT_b = T_b larutan – T_b air

        = 100,15 °C – 100 °C = 0,15 °C

Jadi, derajat ionisasi MgSO₄ adalah 0,8.

b. Untuk menghitung titik bekunya, kita cari dulu penurunan titik bekunya dengan rumus:

T_f larutan = T_f air – ΔT_f

                 = 0 °C – 0,52 °C = –0,52 °C

Jadi, titik beku larutan tersebut adalah –0,52 °C.

Itulah Rumus dan Contoh Soal Penurunan Tekanan Uap Jenuh, Kenaikan Titik Didih, dan Penurunan Titik Beku Larutan Elektrolit yang dapat kami bagikana pada kesempatan kali ini, semoga dapat memberikan manfaat dan dimanfaat dalam pengembangan ilmu pengetahuan Kimia. - RumusKimia.net

Pustaka:

[Kimia IPA Kelas 12 Iman Rahayu]

[Google Images]

[RumusKimia.net]

Related Posts:

Tweet

Sifat Koligatif Larutan Elektrolit

Sifat Koligatif Larutan Elektrolit - RumusKimia.net kali ini akan share materi kimia tentang sifat koligatif larutan elektrolit. Untuk lebih memahami sifat koligatif larutan elektrolit, pelajarilah penjelasan berikut ini.

Sifat Koligatif Larutan Elektrolit

Lihat juga materi Kimia lainnya:

• Penurunan Tekanan Uap Sifat Koligatif Larutan Nonelektrolit.
• Kenaikan Titik Didih Sifat Koligatif Larutan Nonelektrolit.
• Penurunan Titik Beku Sifat Koligatif Larutan Nonelektrolit.
• Tekanan Osmotik Larutan Nonelektrolit.
• Tata Penamaan Trivial atau Nama Lazim pada Senyawa Alkohol.

Sifat Koligatif Larutan Elektrolit

Menurut Arrhenius, suatu zat elektrolit yang dilarutkan dalam air akan terurai menjadi ion-ion penyusunnya sehingga jumlah partikel zat pada larutan elektrolit akan lebih banyak dibandingkan dengan larutan nonelektrolit yang konsentrasinya sama. Hal ini menyebabkan sifat koligatif pada larutan elektrolit lebih besar daripada larutan nonelektrolit.

Perilaku elektrolit dapat digambarkan dengan memerhatikan fenomena di atas. Penurunan titik beku ΔT_f larutan 0,005 m NaCl 1,96 kali (2 kali) ΔT_f glukosa sebagai zat nonelektrolit, demikian juga ΔT_f untuk K₂SO₄ hampir 3 kali dari ΔT_f glukosa. Keadaan ini dapat dinyatakan dengan persamaan berikut.

ΔT_f  elektrolit = i × ΔT_f  nonelektrolit

Hubungan Bilangan Faktor Van’t Hoff dengan Sifat Koligatif Larutan Elektrolit

Van’t Hoff

Hubungan sifat koligatif larutan elektrolit dan konsentrasi larutan dirumuskan oleh Van’t Hoff, yaitu dengan mengalikan rumus yang ada dengan bilangan faktor Van’t Hoff yang merupakan faktor penambahan jumlah partikel dalam larutan elektrolit.

i = 1 + (n – 1) α

Keterangan:

• i = faktor yang menunjukkan bagaimana larutan elektrolit dibandingkan dengan larutan nonelektrolit dengan molalitas yang sama. Faktor i inilah yang lebih lanjut disebut faktor Van’t Hoff.
• n = jumlah ion dari elektrolit
• α = derajat ionisasi elektrolit

Contohnya:

1. Contoh elektrolit biner:

NaCl_(s) →Na⁺_(aq) + Cl^–_(aq)                (n = 2)

KOH_(s) →K⁺_(aq) + OH^–_(aq)                (n = 2)

2. Contoh elektrolit terner:

H₂SO_4(l) + 2 H₂O(l) →2 H₃O⁺_(aq) + SO4^2–_(aq)           (n = 3)

Mg(OH)2(s) →Mg²⁺_(aq) + 2 OH^–_(aq)                             (n = 3)

3. Contoh elektrolit kuarterner:

K₃PO_4(s) →3 K⁺_(aq) + PO₄^3–_(aq)                                   (n = 4)

AlBr_3(s) →Al³⁺_(aq) + 3 Br^–_(aq)                                       (n = 4)

Untuk larutan elektrolit berlaku Hukum Van’t Hoff

Kesimpulan:

Jadi sifat koligatif larutan elektrolit bergantung pada faktor Van’t Hoff.

i = 1 + (n – 1) α

Itulah penjelasan mengenai Sifat Koligatif Larutan Elektrolit yang dapat kami share pada kesempatan kali ini, semoga dapat memberikan manfaat bagi kita semua. Mohon saran jika ada pengembangan materi ataukah ada kekurangan. - Rumus Kimia

Pustaka:

[Prkatis Belajar Kimia IPA Kelas 12 Iman Rahayu 2009.]

[Google Images.]

[RumusKimia.net.]

Related Posts:

Tweet

Contoh Soal Luas Layang-Layang dan Pembahasannya

Contoh Soal Luas Layang-Layang dan Pembahasannya - Sudahkah kalian membaca pembahasan Rumus Matematika Dasar mengenai materi Cara Menghitung Rumus Luas dan Keliling Layang-Layang ? sebaiknya kalian mempelajarinya terlebih dahulu sebelum membaca pembahasan contoh soal yang akan diberikan di dalam materi kali ini karena itu adalah konsep dasar yang dipergunakan untuk menjawab soal-soal di bawah ini. Kalau sudah mempelajarinya, sekarang kita praktekkan langsung untuk menjawab soal-soal berikut ini: 

Contoh Soal dan Pembahasan Luas Layang-Layang

Contoh Soal 1:

Sebuah bangun berbentuk layang-layang dengan panjang diagonal 1(d1) berukuran 18 cm dan diagonal 2 (d2) berukuran 16 cm. Tentukan luas bangun tersebut !

Penyelesaiannya:

Diketahui:  diagonal 1 (d1) = 18 cm

                   Diagonal 2 (d2) = 16 cm

Ditanya : luas (L)

Jawab :

 

Jadi luas bangun tersebut adalah cm²

Contoh Soal 2:

Layang-layang memiliki luas 280 cm² dan salah satu diagonalnya berukuran 20 cm. Tentukan ukuran diagonal yang lain!

Penyelesaiannya:

Diketahui:  diagonal 1 (d1) = 20 cm

                   luas (L) = 280 cm²

Ditanya : Diagonal 2 (d2)

Jawab :

 

Jadi panjang diagonal yang lainnya adalah 14 cm

Contoh Soal 3:

Deni akan membuat layang-layang. Dua potong bambu yang Deni pakai berukuran 30 cm dan 22 cm. Apabila layangan sudah jadi, berapakah luasnya?

Penyelesaiannya:

Diketahui:  diagonal 1 (d1) = 30 cm

                   Diagonal 2 (d2) = 22 cm

Ditanya : luas (L)

Jawab :

 

       Jadi luas layang-layang tersebut adalah cm2

Contoh Soal 4:

Aldo memiliki kertas berukuran 60 cm x 100 cm. Kertas itu ia gunakan untuk membuat 6 buah layang-layang yang berukuran 36 cm x 40 cm. Berapa luas kertas yang tersisa?

Penyelesaiannya:

Diketahui:  ukuran kertas = 60 cm x 100 cm

  diagonal 1 (d1) = 36 cm

                   Diagonal 2 (d2) = 40 cm

Ditanya : luas kertas tersisa (L)

Jawab :

 

        Luas kertas = 60 x 100 = 6000 cm²

Luas layang –layang =

Kertas terpakai = 6 x 720 = 4320 cm²

Kertas tersisa = 6000 cm² - 4320 cm² = 1680 cm²

Jadi luas kertasa yang tersisa adalah 1680 cm²

Contoh Soal 5:

Di rumah Mira terdapat hiasan dinding berbentuk layang-layang dengan ukuran luas 420 cm².  Jika salah satu diagonalnya berukuran 28 cm tentukanlah ukuran diagonal yang lainnya!

Penyelesaiannya:

Diketahui:  diagonal 1 (d1) = 28 cm

                   luas (L) = 420 cm²

Ditanya : Diagonal 2 (d2)

Jawab :

  

Jadi panjang diagonal yang lainnya adalah 30 cm

Itulah 5 Contoh Soal Luas Layang-Layang dan Pembahasannya yang dapat kalian pelajari untuk memahami langkah-langkah mudah di dalam menjawab soal-soal matematika mengenai luas layang-layang. Semoga bisa membantu kalian yang masih bingung mengenai cara mengerjakan soal-soal serupa. Sampai jumpa lagi di dalam pembahasan soal-soal lainnya.

Related Posts:

Tweet

Cara Mudah Menghitung Luas Permukaan Bidang Empat Beraturan

Cara Mudah Menghitung Luas Permukaan Bidang Empat Beraturan - Apakah yang disebut sebagai bidang empat beraturan? bidang empat beraturan merupakan bangun ruang yang terdiri atas empat bidang sisi yang bentuknya berupa segitiga sama sisi. Bidang empat beraturan lebih umum dikenal sebagai limas segitiga beraturan karena keseluruhan sisinya berbentuk segitiga sama sisi. Lalu bagaimanakah cara menghitung luas permukaan bidang dari limas segitiga ini? simak pembahasan Rumus Matematika Dasar di bawah ini:

Cara Cepat Mencari Luas Permukaan Bidang Empat Beraturan

Pertama-tama kalian harus memperhatikan gambar limas segitiga sama sisi (bidang empat beraturan) T.ABC berikut ini:

Bila diperhatikan, pada bangun ruang di atas terdapat empat buah segitiga sama sisi yang luasnya tentu saja sama. Segitiga sama sisi itu adalah ΔABC, ΔBCT, ΔACT, dan ΔABT. Rumus mudah dan cepat untuk menghitung lkuas segitiga sama sisi tersebut adalah:

 L.Δ = ¼s2√3

Ada empat permukaan bidang empat (limas segitiga sama sisi) dengan luas yang sama pada gambar di atas, maka:

L = 4 × L.Δ

L = 4 × ¼s²√3

L = s²√3

Jadi, rumus untuk mencari volume (V) bidang empat beraturan yang memiliki panjang rusuk (s) adalah:

L = s²√3

Contoh Soal 1:

Diketahui sebuah bidang empat beraturan mempunyai panjang rusuk 8 cm. Berapakah  luas permukaan bidang empat beraturan tersebut?

Penyelesaiannya:

L = s²√3

V = (6 cm)²√3

V = 64√3 cm²

Jadi, luas permukaan bidang empat beraturan tersebut adalah 64√3 cm²

Itulah Cara Mudah Menghitung Luas Permukaan Bidang Empat Beraturan (limas segitiga sama sisi) apabila panjang rusuknya telkah diketahui. Semoga saja kalian bisa memahami penjelasan di atas dengan baik.

Related Posts:

Tweet

Contoh Soal dan Pembahasan Cara Menghitung Jarak Titik ke Garis Pada Kubus

Apakah kalian sudah membaca postingan Rumus Matematika Dasar mengenai Cara Menghitung Jarak Titik ke Titik, Garis, dan Bidang ? jika belum, sebaiknya membacanya terlebih dahulu agar kalian bisa lebih mudah memahami Contoh Soal dan Pembahasan Cara Menghitung Jarak Titik ke Garis Pada Kubus yang akan dijelaskan di bawah ini:

Contoh Soal dan Pembahasan Cara Menghitung Jarak Titik ke Garis Pada Kubus

Contoh Soal 1

Diketahui panjang rusuk sebuah kubus ABCD.EFGH adalah 6cm. Maka hitunglah jarak:

a).titik D ke garis BF
b).titik B ke garis EG

Penyelesaiannya:

a).Agar lebih mudah dalam menjawabnya, mari kita perhatikan gambar di bawah ini:

Dari gambar di atas kita bisa melihat bahwa jarak titik D ke garis BF adalah panjang diagonal BD yang dapat ditentukan dengan menggunakan teorema phytagoras ataupun dengan rumus. Mari kita selesaikan dengan teorema phytagoras terlebih dahulu:

BD2 = AB² + AD²
BD2 = 6² + 6²
BD2 = 72
BD = √72 = 6√2 cm

beikut bila kita mencarinya dengan menggunakan rumus:

d = s√2
BD = AB√2
BD = (6 cm)√2
BD = 6√2 cm

Maka, jarak titik D ke garis BF adalah 6√2 cm



b). Sama halnya dengan soal a) kita juga harus membuat gambarnya terlebih dahulu agar lebih mudah mengerjakannya.

Dari perhitungan pada soal a) diketahui bahwa panjang diagonal sisi kubus FH = BD adalah 6√2 cm

Untuk mengetahui panjang BP, kita gunakan teorema phytagoras untuk segitiga siku-siku BFP:

FP = ½ FH = 3√2 cm

maka:

BP2 = FP² + BF²
BP2 = (3√2)² + 6²
BP2 = 18 + 36
BP2 = 54
BP = √54 = 3√6 cm

Maka,jarak titik B ke garis EG adalah 3√6 cm

Sekian pembahasan tentang  Contoh Soal dan Pembahasan Cara Menghitung Jarak Titik ke Garis Pada Kubus. Sampai jumpa lagi di dalam pembahasan contoh soal yang lain. Semoga kalian dapat memahami dengan baik apa yang sudah dijabarkan di atas.

Related Posts:

Tweet